인공신경망 학습
- 입력값과 해당 노드의 가중치를 곱한 후 모두 합산
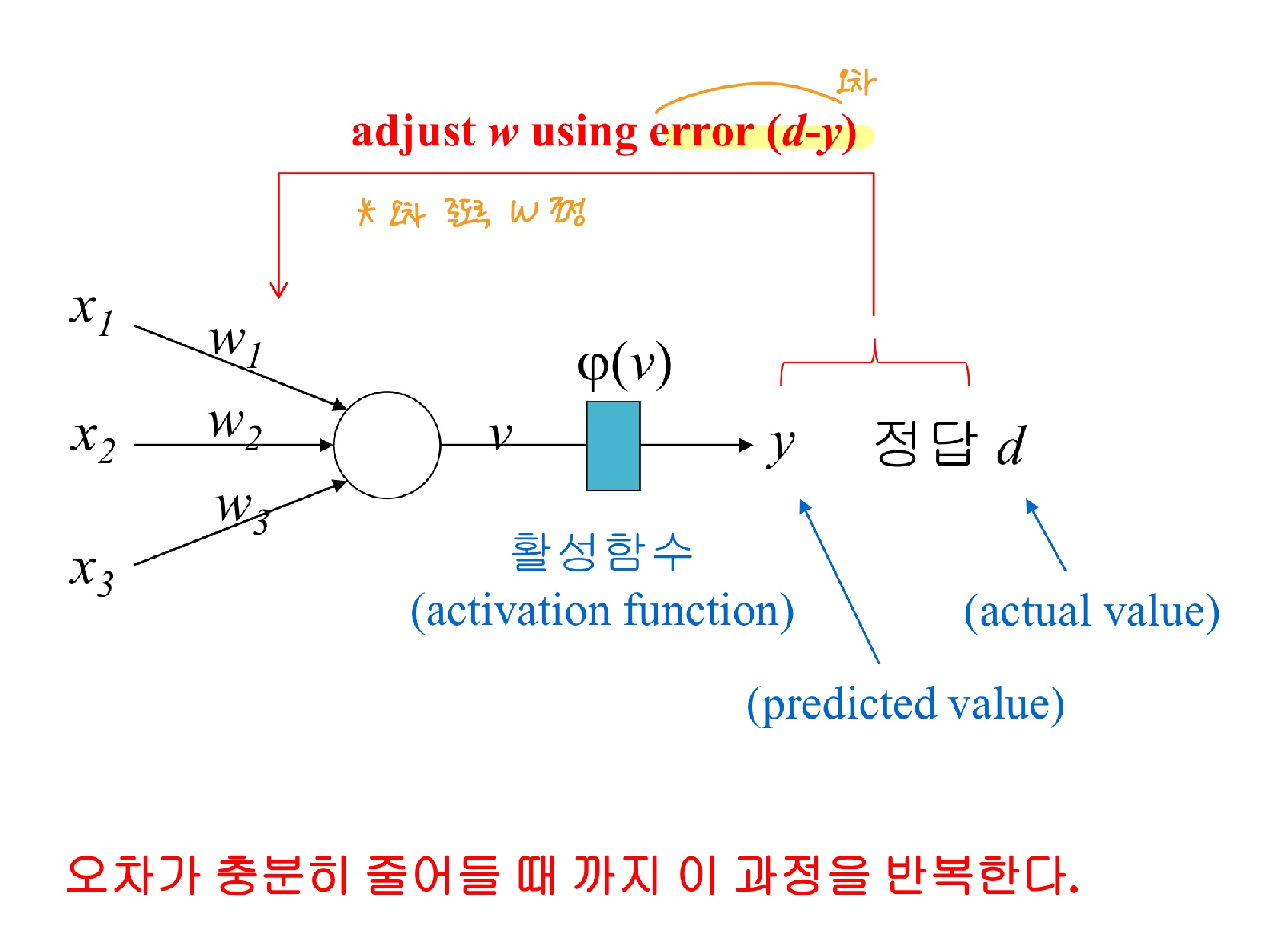
- 합산한 결과를 가중합(v) 이라고 함

- 가중합을 0~1 사이의 값으로 바꿔주기 위해서 활성 함수를 사용
- 예측값과 실제 정답의 오차를 이용해 가중치를 조정하는 과정을 반복
💡 Activation Function
- 가중합 v 를 0~1 사이의 값으로 변환
- 여러 함수가 사용될 수 있음
1) sigmoid 함수
- 자신의 노드로 들어오는 신호의 가중합만 고려
- 보통 출력이 이진수(0,1)일 때
import numpy as np
def SIGMOID(x):
return 1/(1 + np.exp(-x))
2) softmax 함수
- 출력 노드가 여러 개 일 때 자신의 노드 뿐 아니라 다른 노드로 들어오는 신호의 가중합도 고려
- 출력 노드가 여러 개 일 때 용이

import numpy as np
def SOFTMAX(x):
e_x = np.exp(x) #e^x
return e_x / e_x.sum(axis=0)
- 나는 보통 0,1 이진값으로 출력이 나오도록 예측 모델을 만드는 경우가 많다. 이때 출력 노드를 하나로 해서 해당 가중합이 0.5 를 넘어가는지 여부에 따라 0,1 을 결정할 수 도 있고, 출력 노드를 2개 만들어서 더 확률이 높은 노드의 이진값을 결과로 낼 수가 있다. (one-hot encoding도 사용)
💡Learning Rate
- 학습률 (0<α≤1)
- α가 작으면 w의 변동폭 작다 ⇒ 정답에 보다 근접할 수 있지만 학습시간이 길어지거나 정답 근접 전에 max iteration limit에 걸려 학습 중단될 수 있음
- α가 크면 w의 변동폭 크다 ⇒ 학습 시간이 짧아지지만 정답에 수렴 못하고 발산할 수 있음
💡Delta rule
- 예측값과 정답 사이의 오차(에러값→cost function으로 구함)를 가지고 w 를 조정하는 방법
- 입력값이 크면 가중치 조절 정도도 크다(반영 정도가 크다)
- backpropagation
- 경사하강법 사용
- 활성함수에 따라 가중치 조정 정도가 조금씩 달라짐
(1) 활성 함수가 φ(v) = v 일 때,
W(after) = W(before) +α x 에러값 x 입력값
* α는 학습률(0<α≤1)
→ w의 변동폭을 조절해준다.
α가 크면 변동폭이 크기에 정답에 금방 접근할 수 있고 학습 시간이 짧아질 수 있지만 정확히
수렴하지 못하고 발산할 수가 있고, α가 작으면 변동폭이 작아 보다 정답에 세심하게 접근할 수
있지만 학습 시간이 길어지고 max iteration limit(반복 횟수 제한)에 걸려 멈출 수 있다.
(2) 활성 함수가 φ(v) = v 이 아닐 때, ⇒ 일반화된 식 필요
W(after) = W(before) +α x φ’(v) x 에러값 x 입력값
(활성함수의 도함수에 출력값을 넣어 계산한 결과를 함께 곱해준다)
사실 활성 함수가 φ(v) = v 인 경우에도 미분 해보면 φ’(v) = 1 이기 때문에 (1)이 되는 것이다.
만약 활성 함수로 sigmoid 함수를 사용한다면 φ’(v) = φ(v)(1-φ(v)) 가 될 것이다. 그리고 φ(v) 는 y 라고도 표현하기 때문에 W(after) = W(before) +α x y(1-y) x 에러값 x 입력값 라고 표현할 수도 있다.
W(after) = W(before) +α φ’(v) e x
W(after) = W(before) +α φ(v)(1-φ(v)) e x
W(after) = W(before) +α y(1-y) e x
✔️ Delta Rule과 경사하강법(Gradient Descent)
오차가 줄어드는 방향으로 w(delta)를 update 하기 위해 미분
미분을 해주면 기울기를 얻을 수 있고 이 기울기에 따라 w를 업데이트
경사하강법을 통해 알 수 있는 2가지가 있다.
(1) 기울기가 음/양 인지에 따라 에러가 정답보다 더 큰지 작은지 방향을 알 수 있다.
(2) 기울기의 크기에 따라 W를 조절할 수 있다.
기울기가 크면 그만큼 w의 변동 정도도 커진다는 의미이다. w의 변동 정도 혹은 반영 정도를 조절
해주는 방법으로는 학습률 α도 있었다. w 변동이 너무 크거나 작으면 문제가 되기 때문에 기울기
를 확인하고 학습률을 조절 해주는게 좋다.
💡 Cost Function(=loss function)
- 오차를 계산하는 방법
- 오차를 어떻게 계산 하느냐에 따라 W가 달라지고, 학습 속도가 달라짐
1) MSE: Mean of square error
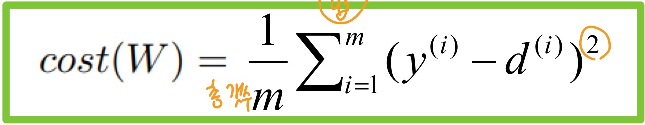
- Sum of square error
- neural network 에서 전형적으로 쓰임
2) Cross Entropy

- d = 0 , 1 일 때 각 항이 사라짐
- 가중치 갱신을 기울기에 따라 갱신하지만 cross entropy의 경우, log 함수 이기 때문에 초기엔 기울기 경사 폭이 급격하고 그에 따라 초기 error는 확확 줄어듬 (후반에 매우 조금씩 준다)
⇒ 발산하거나 학습 시간이 너무 길어지는 단점 보완
💡 Weight 갱신
1) Stochastic 경사하강법(SGD; stochastic gradient decent)
- 매번 오차와 가중치를 계산해 업데이트
- 오차가 빨리 줄어들지만 갱신이 너무 자주 일어남
2) 배치(batch)
- 매번 오차와 가중치를 계산하고 한 번 반복 끝날 때마다 평균값으로 가중치 한 번 업데이트
- 갱신 속도, 학습 속도 느림
3) 미니배치(mini batch)
- SGD와 배치 방식의 중간
- 전체 학습 데이터를 일정 크기로 묶어서 해당 묶음이 끝나면 평균값으로 갱신
- 오차를 가장 많이 줄여줌
💡 Epoch
- 전체 학습 데이터를 한 번씩 모두 학습 시킨 횟수(반복 횟수)
'인공지능(AI) & 데이터 분석' 카테고리의 다른 글
| [Feature Engineering] Feature Selection & evaluation (0) | 2022.11.23 |
|---|---|
| [Feature Engineering] Data pre-proceessing (데이터 전처리) (0) | 2022.11.22 |
| [CNN/이미지처리] 데이터 증강(Data Augmentation) (0) | 2022.04.14 |
| 논문 (빨리)(효율적으로) 읽는 법 *다시 정리 예정 (0) | 2022.03.11 |
