💡그래프
- 경로 : 두 노드 사이에 이음선으로 연결된 노드의 나열
- 연결 그래프
- 부분그래프
- 방향성/비방향성 그래프 :
- 경로 :
- 순환경로 :
💡신장트리
- 연결된 비방향성 그래프에서 순환경로가 없어지도록 이음선을 제거해 구성한 그래프
- 모든 정점을 다 포함하되 순환경로가 존재하지 않는 연결 그래프
💡MST (최소비용 신장 트리)
- 신장 트리가 되는 부분그래프 중에서 가중치의 합이 최소가 되는 그래프
- 순환경로X
ex) 도로건설, 통신, 배관
- MST를 찾기 위한 알고리즘으로는 무작정 알고리즘, 탐욕적 알고리즘, 프림 알고리즘, 크루스칼 알고리즘 등 존재
무작정 알고리즘 : 모든 경우 다 고려
탐욕적 알고리즘 : 적절한 최적해 선정절차 따라 하나의 이음선 선정(선정) -> 순환경로 생기지 않는지 확인 후 추가(적절성 점검) -> 결과 부분그래프가 신장트리면 최소비용신장트리
💡Prim Algorithm
- 정점에 인접한 이음선 중 가중치가 최소인 것을 선정, 순환경로 생기면 다음 이음선 선택
✔️복잡도
T(n) = 2(n-1)(n-1) = O(n^2)
정리.
💡Kruskal Algorithm
- 가중치를 올림차순하여 하나씩 선택, 순환경로 생기면 다음 이음선을 선택
정리.
💡Dijkstra Algorithm
- 현재까지 알고 있던 최단 경로를 계속해서 갱신
- 시작 정점에서 다른 정점으록 가는 최소 가중치를 계속 갱신
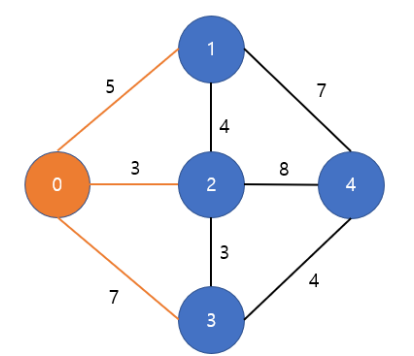
| 정점 | 0 | 1 | 2 | 3 | 4 |
| 가중치 | 0 | 5 | 3 | 7->6 | INF |
예를 들어 정점 0을 시작점이라 한다면 시작점에서 각 노드로 갈 수 있는 최소 경로를 갱신한다.
시작점에서 정점 3으로 가는 방법을 보면
처음에는 정점 0에서 바로 갈 수 있는 방법을 선택하면 가중치가 7이 되지만
다음단계에서 정점 2를 방문하고 방문하면 가중치가 6이 된다.
https://code-lab1.tistory.com/29
[알고리즘] 다익스트라(Dijkstra) 알고리즘이란? | c++ 다익스트라 구현
다익스트라(Dijkstra) 알고리즘이란? 다익스트라 알고리즘은 그래프 상에서 시작 정점부터 나머지 각 정점까지의 최단거리를 계산하는 알고리즘이다. 다익스트라 알고리즘은 그래프의 어느 간선
code-lab1.tistory.com
'알고리즘 > 알고리즘 이론' 카테고리의 다른 글
| [알고리즘]동적 계획(Dynamic Programming)_최단거리 Floyd - Warshall (2) | 2022.06.13 |
|---|---|
| [알고리즘]동적 계획(Dynamic Programming)_이항계수 (0) | 2022.06.13 |
| [알고리즘] 탐욕 알고리즘 (Greedy Algorithm) (0) | 2022.04.14 |
| [알고리즘] 분할 정복 - 행렬의 곱셈, 마스터 정리, 쉬트라쎈 (0) | 2022.04.14 |
| [알고리즘] 분할정복 - Quicksort(빠른정렬) (0) | 2022.04.13 |
